Send waves down a spring and watch them travel.
Send waves down a spring and watch them travel.
Introduction
This exploration begins by observing how pulses travel along a stretched spring. Then it continues by measuring the speed of the pulses and how the speed depends on the length and height of the pulse and the tension in and mass per unit length of the spring. Finally, two pulses are observed as they pass through each other.
Materials
Optional, paper, pencil, and a calculator
a spring scale able to read up to 10 N
accurately
a scale to weigh the cord
a slinky
(You can also use a snaky spring in place of the phone cord. If you
use a snaky spring you will need to attach a carabiner to the metal
loops at each end to serve as a handle, if you use a metal coil
spring you MUST use a safety wrist loop, a piece of cord tying
the end of the spring to each participants wrist.)
One pulse
To Do and notice
Make pulses on the cord and watch them move.
One person sends a pulse down a phone cord.
Have your partner hold one end of the phone cord
or attach it firmly in place at about waist height.
Stretch the phone cord to a length between 3 and 5 meters.
Jerk the hand holding the cord to the right about one handspan, about
25 cm, then immediately return your hand to its original
position.
Notice that a rightward pulse travels down the cord.
A leftward pulse returns down the cord after bouncing at the far
end.
What's Going On?
What moves down the cord?
Motion moves down the cord, the motion of bits of the cord to the
right and back.
In addition,
Energy, moves down the cord. The kinetic energy of the parts of the
cord moving side to side plus the potential energy of the deformed
cord. Your partner could absorb the energy of the pulse and use it to
do work.
Momentum moves down the cord. When the pulse reaches the end of the
cord it exerts a force on the end to the right and then back to the
left because the pulse carries sideward momentum.
The official scientific name for what moves down the cord is
displacement. The displacement of the coils from their rest position
moves down the cord.
Two pulses adding together
Lay the cord on the ground and stretch it to 4
meters. Place an empty paper or styrofoam cup next to the center of
the cord.
Send a pulse down the cord that will hit the cup and knock it
over.
While you send a pulse toward the cup (move your hand to the right)
have your partner send an identical pulse away from the cup (They
move their hand toward your left). The pulses will arrive at the
center at the same time, the rightward pulse will add to the leftward
pulse canceling it. The sum of the waves will be zero the waves will
miss the cup, and the cup will remain standing.
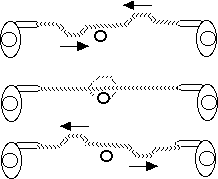
Two people can send pulses in opposite directions so that the pulses cancel just as they pass an object located in the center of the cord.
Etc.
Just like waves on the cord, two sound waves can add together and cancel. Arthur C. Clark once wrote a story of a machine which produced sound waves which canceled other sound waves to create quiet. The pilots aboard the Voyager aircraft wore headphones which created sound waves which added to the sounds of the aircraft and canceled them. Sounds which cancel noise are called anti-noise.
Measuring wave speed
Measure the speed of the pulse, v.
To do this,
Measure the length of your cord, d,
and the time it takes a pulse to move the length of the cord, t.
The time is best measured with a stopwatch by the person who sends
the pulse.
The speed is length divided by time
It will take about half a second for the pulse to travel the length of the cord. If the length is 4 m then the speed will be about 8 m/s. This will be difficult to measure precisely. However, after the next two activities you will be able to measure the speed more accurately.
Measure the speed of the pulse as a function of the length of the pulse. Move your hand 25 cm to the side as rapidly as possible to make a pulse which is short in length as well as in time.
Then move your hand 25 cm to the side and back more slowly.
Long pulses move at the same speed as short pulses
Theoretically, and practically, the speed of your
pulse is independent of the length of your pulse.
How fast you move your hand to the side has nothing to do with how
fast the pulse travels along the cord.
Reach out along the cord about 25 cm and pull it to the side 25 cm and hold it.
Pull the cord to the side, make a pulse by releasing it.
Release the cord.
Measure the speed of the pulse.
The pulse which starts from rest travels at the same speed as the
pulses which start as jerks.
Measure the speed of the pulse as a function of its height. Make a pulse by moving your hand 10 cm (about a fist width) to the side. Then make a 25 cm high pulse. Then a 50 cm pulse.
Large amplitude pulses travel at the same speed as small amplitude pulses.
The speed of the pulse should be independent of
its amplitude.
(It's more complicated than that. For large pulse heights the speed
may show a slight increase since pulling the cord far to the side
increases the tension in the cord.)
Since the speed of pulses is independent of their size you can improve the accuracy of your timing by sending a pulse and allowing it to travel down the string to your partner and back 5 times. The pulse travels down and back so it travels the length of the cord 10 times. The speed of the pulse is the 10 times the length of the cord, d, divided by the time for 10 one way trips.
v = 10 d/T (for 5 round trips)
To time ten one-way trips start the pulse as you count zero, then count one, two, three, four, five counting once each time the pulse returns.
Note it is really important that when you start the pulse you count ZERO, then on the first return ONE, and so on. Otherwise your count will be off-by-one, and you'll get the wrong speed.
Speed, Tension, and Density
To complete the quantitative part of this activity you will need a spring scale.
Stretch the cord until it is 4 meters long.
Measure the speed of the pulses on the cord. Remember that the speed
does not depend on the amplitude so you can measure the time it takes
the pulse to make 5 round trips or ten lengths of the cord, then get
the time it takes to travel one length, four meters, by dividing the
total time by 10.
Next, stretch the cord to 3 meters long and measure the speed.
Finally, stretch the cord to 5 meters and measure the speed.
(Optional you can measure the speed at 6, 7, and 8
meters.)
The speed increases as the cord is stretched. Theory says that the speed of the wave increases as the tension in the cord increases, and that it also increases as the mass per unit length of the cord decreases. As you stretch the cord you increase the tension and decrease the mass per unit length so that the speed definitely increases.
The theory says that
where
v is the speed of the pulse on the cord.
T is the tension in the cord.
m/L is the mass per unit length of the cord.
Measure the mass of the cord, m, in kilograms then compute the mass per unit length.
For example our cords have a mass of 0.5 kg and so when stretched to 4 meters they have a mass per unit length of 0.12 kg/m or 1/8 kg/m.
Measure the tension in the cord with a spring scale. To stretch our cords to 4 m requires 8 newtons of tension.
The predicted speed of our pulse is
v = (T/m)0.5 = (8/(1/8))0.5 = 8 m/s
the measured speed is
v = 8 m/s.
Stretching the cord to 6 meters from 3 meters doubles the length of the cord, cuts the mass per unit length in half (it is, after all, the same cord.) and increases the tension to double the original tension (or more.)
If the tension were to double exactly, then the
speed of the pulse would double.
(2 /(1/ 2))0.5 = 2.
The time it takes for a pulse to travel the length
of the cord would remain the same!
The pulse has to travel twice as far, at twice the speed, so the time
remains the same.
In reality, the speed more than doubles so that the time it takes the
pulse to travel the length of the cord decreases slightly when the
cord is stretched.
|
Scientific Explorations with Paul Doherty |
|
25 May 2000 |