
The small balloon universe. Each dot is a cluster of galaxies.
Notice the triangle.
Expanding balloon universe
Introduction
Inflating a balloon can model the expansion of the universe.
Material
To Do and Notice
Blow up a balloon until it is firm yet small.
Stick on a half dozen dots at random.
Each dot represents a cluster of galaxies, a hundred million light
years across.

Pick one dot to be the cluster of galaxies that we live in, label it A.
Label the nearest galaxy to A, B.
Label the second nearest galaxy C.
Measure the distance along the surface of the balloon from A to B.
(Imagine two-dimensional beings, flat ants or flants, living in the clusters. To the flants there is no other distance except for the distance along the balloon they cannot imagine the shortcut through the third dimension. Just like we creatures of three-dimensions find it hard to picture four dimensional space.)
Measure the distance from A to C.
Blow up the balloon until the distance from A to B is double the original distance.

Measure the distance from A to C.
Notice the distance from A to C has also doubled.
For example if A to B is 5 cm and you blow up the balloon until it is 10 cm.
Then the distance from A to C which might have been 9 cm will grow to 18 cm.
If you plot these points on a Hubble diagram of velocity versus distance assuming you blow up the balloon in 1 second, then the velocity of A to C expansion (10-5) cm/1 s will be plotted against the initial distance to A, 5 cm. Similarly, the velocity of C with respect to A is (18-9) cm/1s will be plotted against 9 cm. Both of these points lie on a straight line through the origin.
Repeat the experiment using all of your dots and notice that they lie on a straight line in a Hubble Plot.
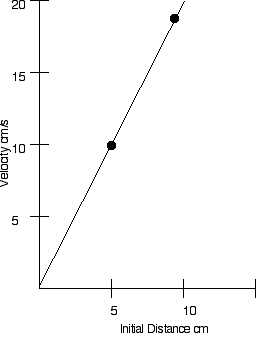
What's Going On?
If the universe is expanding uniformly so that the distance between every two points grows by the same fraction in every time interval, as points stuck to a balloon do, then these points will lie on a straight line in a Hubble plot.
When the recession velocity of galaxies is plotted versus distance out to 1.5 billion light years the points lie on a straight line.
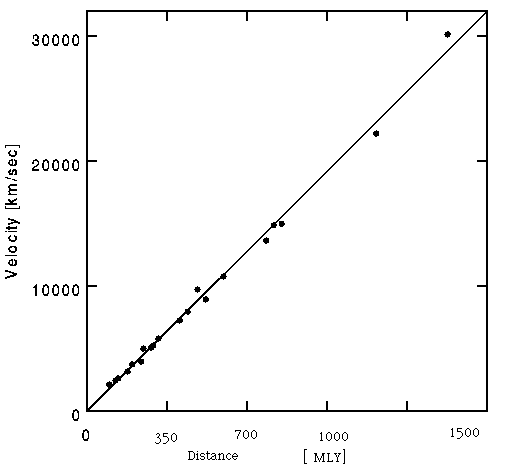
Going Further
In the balloon model space is two dimensional, it only exists on the surface of the balloon.
The two-dimensional space exists in three dimensions. With time the space expands into the third dimension.
In the future the balloon will have larger radius.
In the past it had a smaller radius.
The inside of the balloon represents the past.
A perfect balloon, like a perfect universe, starts from a tiny region and expands.
The center of the balloon is the big bang, a small region in space which contained the entire universe when it began.
All of the points on the balloon were together at the center during the big bang.
In our three-dimensional universe we see the distances between galaxy clusters increasing with time. Our three-dimensional universe is expanding in four dimensions.
Etc.
It is better to use stick-on dots than to draw dots on the balloon because this models the behavior of galaxy clusters which do not expand as the Universe expands. The distance between the stick on dots changes, but the size of the dots does not change as the balloon inflates.
|
Scientific Explorations with Paul Doherty |
|
18 Jan 2001 |