Zeno Knows
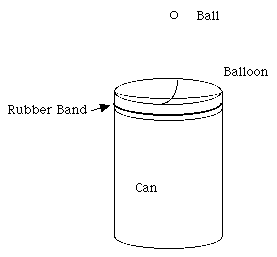
A ball dropped on a balloon stretched across an open topped
can will bounce a long time.
Zeno Knows

A ball dropped on a balloon stretched across an open topped
can will bounce a long time.
Introduction
A steel ball bounces well on a concave rubber membrane. As the ball bounces repeatedly its height diminishes and the time interval between successive bounces becomes shorter.
Material
a small ball bearing 0.5 cm diameter to 1cm diameter (1/4" to 1/2")
A "tin" can (like a soup can)
a can opener
A balloon
A rubber band
a hammer and nail (or a drill)
tape
Assembly
Use the can opener to remove one end of the can completely, discard the end.
Remove the material in the can, optional, eat it.
Use the hammer and nail to poke a hole in the bottom of the can. (drill a hole in the bottom.)
Cut the balloon open and stretch one layer of rubber over the open can, hold it in place with a rubber band.
Poke down in the center of the balloon about 2 cm (1") forcing air out the hole in the bottom of the can. Cover the hole in the bottom with a piece of tape. Release your pressure on the balloon.
You now have a tin can with a concave rubber membrane over one end. Place it on the table with the balloon-covered end up.
To Do and Notice
Drop the steel ball onto the middle of the balloon.
Notice how it continues to bounce.
Notice that if it bounces off toward one side, the concave shape of the balloon sends it bouncing back toward the center.
Notice that each bounce is slightly less high than the previous bounce, and that each bounce is the same fraction of the previous bounce.
Notice that the bounces happen more rapidly as time goes by.
What's Going On?
When you first drop the ball its gravitational potential energy is converted into kinetic energy. It reaches its maximum speed just about as it hits the surface of the balloon. Very little energy is lost when the steel ball bounces off the rubber membrane. So it bounces back up with just about the same speed with which it came down.
Since the ball loses so little energy with each bounce it goes on bouncing for a long time.
It does lose a little energy each time so each bounce is lower than the previous bounce. Measurements show that each bounce is a constant fraction of the height of the previous bounce. Each bounce takes a shorter time than the previous bounce. The frequency of the balls bounces becomes higher and higher.
Math Root
First some definitions
The potential energy of the ball at the top of each bounce is Ep = mgh
where m is the mass of the ball,
g is the acceleration of gravity, and
h is its height above the balloon.
The kinetic energy as the ball hits the balloon is Ek = 0.5 mv2
where v is the speed of the ball.
The ratio of the outgoing speed, V1, to the incoming speed, V0, is called
the coefficient of restitution, Cr = V1/V0
The kinetic energy as the ball hits the balloon is the same as the potential energy at the top so the velocity of the ball is related to the height: 0.5mv2 = mgh
so Cr = V1/V0 = Sqr(h1/h0)
or h1/h0 = Cr2
where h0 is the height from which the ball is dropped and h1 is the height after the first bounce. Thus the ratio of one height to the previous height is the coefficient of restitution squared.
Now the first math challenge.
Measure the coefficient of restitution for your ball and can.
You can try to measure the eight before and after one bounce and use the square root of the ratio to calculate the coefficient of restitution, but you might get a better answer if you drop the ball from a measured height and then measure the height after 10 bounces. Assume that the coefficient of restitution is a constant. So if the height after n bounces is hn then
h10/h0 = h10/h9 * h9/h8 * h8/h7 * h7/h6 * h6/h5 * h5/h4 * h4/h3 * h3/h2 * h2/h1 * h1/h0
Since all of these ratios are the same then
h10/h0 = (h1/h0)10
Since each of these terms is the square of the coefficient of restitution, h10/h0 = Cr2, we get
h10/h0 = (Cr2)10
or solving Cr = (h10/h0)1/20
The coefficient of restitution is the twentieth root of the ratio of the height of the 10'th bounce divided by the height from which the ball was first dropped.
alternate solution Count the number of bounces, n, until the height of the bounce has become 1/2 of the initial height.
hn/h0 = 1/2
Math note, When something decreases by the same fraction, f, at each step it follows an exponential decrease.
from above hn/h0 = (Cr2)n
solve for the number of bounces, n, needed to reduce the height to 1/2 the original height.
1/2 = (Cr2)n
or (1/2)1/(2n) = Cr
so (1/2n)log (1/2) = log (Cr)
n = 0.5 log (1/2)/log(Cr)
check this , if Cr = sqr(1/2) then n = 0.5 log(1/2)/log ((1/2)1/2) = 1
Second math challenge
If the ball has a coefficient of restitution of 1/2 and if the time from the first bounce from the rubber to the next contact with the rubber is t1 = 1/2 second, then how long will the ball keep bouncing? and how many times will the ball bounce in this time?
The time, t, it takes a ball to drop from a height h is found from the equation
h = 1/2 g t2
so that t = sqr(2h/g)
Call the time for the first complete bounce from rubber to rubber t1 with height h1 then
t1 = 2sqr(2h1/g)
since the ball must rise up to its height h1 then drop down the same distance.
The second bounce goes to height h2 = h1 Cr2
and takes a time t2 = 2 sqr(2h2/g)
the ratio of t2 to t1 is t2/t1 = 2 sqr(2h2/g)/(2sqr(2h1/g)) = sqr(h2/h1) = sqr(Cr2) = Cr
This is the joy of using the coefficient of restitution.
If the first bounce took t1 = 1/2 second then the second bounce took
t2= 1/2* 1/2 = 1/4 second
and the third bounce took
t3 = t2 * 1/2 = 1/8 second and so on.
Each bounce takes half as long as the previous bounce.
This means there are an infinite number of bounces! No matter how many bounces there have been, the height of the bounces never goes to zero.
However, we can find the total time for the infinite number of bounces by summing all of the individual times
T = Sn=0• tn = 1/2 + 1/4 + 1/8 + ...
The sum of this series is well known and it is 1.
It takes one second for the ball to complete an infinite number of bounces.
Well, actually, the real ball stops bouncing before it makes an infinite number of bounces because the meaning of a bounce becomes unclear when the ball never leaves the rubber of the balloon. So physics saves us from infinity once again.
Etc.
This infinite series with a finite sum is a form of Zeno's paradox.
You can read more about the mathematics of the bouncing of real balls in the complete mathematics root available in the book Math Roots.
Going Further
You can record the sound of the bouncing ball on a computer and then analyze the bounces.
Here is my recording of a steel ball bouncing on a steel plate. It is an mp3 file.
|
Scientific Explorations with Paul Doherty |
|
17 April 2001 |