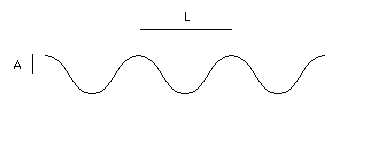
A sine wave with wavelength L, and amplitude A
Peering at waves
Measure the frequency and wavelength of a water wave then compute its velocity.

Material
To Do and Notice
Space the people out along the pier, start them spaced with two meters between their noses.
Observe the waves. Notice their crests and troughs.
Estimate the Amplitude
The amplitude of the wave, A, is the distance in
meters between the center of the wave and its crest.
Surfers measure the wave height between the bottom of the trough and
the top of the wave. The scientists amplitude is thus half of the
surfers wave height.
Measure the Period
Time the period between the passing of one crest and the next (on shore you can also time the period between breaking waves.)
This is the period, T, of the wave in seconds.
Measure the periods between several waves, the
period will vary.
Find the average period. (See the Math
Root)
Buoys out in the ocean measure the period of waves the reports from these buoys can be found on the Internet.
Compute the Frequency
The frequency of the wave is the number of cycles per second and is one over the period.
f = 1/T
So if the period is 10 seconds the frequency is 0.1 cycles per second or 0.1 hertz.
Wavelength
When a crest passes in front of an observer have
them raise their hand.
When a trough comes by have them lower their hand.
Notice the pattern of raised hands on the pier.
The wavelength of the waves is the distance between adjacent wave
crests, which is the distance between two people with raised
hands.
(If the wave is so long in wavelength that only one person has a hand
up at a time space the observers farther apart.)
Measure the wavelength, L.
When two people have their hands raised shout "freeze."
Then measure the distance between them in meters.
Do this for several waves and average your result.
Measure the velocity
Watch the wave crest move down the line of hands.
Measure the velocity of propagation of the wave crest by measuring the time, t, it takes the crest to move a known distance, d. Then calculate:
v = d/t
Compute the Velocity
You can also compute the velocity of the waves from your measurements of the average period and wavelength. First, calculate the average frequency from the average period.
The velocity of the wave is the frequency times the wavelength.
v = fL
The velocity is thus one wavelength divided by the time it takes for the wave to travel one wavelength.
What's going on?
A non-breaking water wave can be approximated by a sine wave with a wavelength, L, a period, T, a frequency, f, and an amplitude, A.
See the Math Root for information on how to write an equation for this sine wave.
Picture a long linear pile of water magically frozen in place above the surface of the ocean. Release the pile. Gravity pulls the pile down. It falls under gravity gaining speed downward and spreading as it falls. When the crest has reached the original flat surface of the water it is traveling rapidly down, it overshoots this position and pushes down a trough in the water. The water from the trough also spreads to the sides creating a crest to both sides of the original pile. The original wave has spread to the side. The gravitational pull of the earth and the inertia of the motion of the water both played a role in the creation of the moving wave crest. This type of water wave is called a gravity wave.
There is another type of water wave in which the crests are pulled down by the surface tension of the water. Surface tension drives waves shorter in wavelength than a few centimeters. So the big waves we see on the ocean are gravity waves.
Waves in the ocean are powered by wind. The wind first builds surface tension waves. It then pushes on the surface tension waves giving them energy, increasing their amplitude and wavelength until they become gravity waves. If you destroy the surface tension of water by coating it with a thin film of oil or soap you can reduce the surface tension waves and reduce the coupling between the winds and the waves creating a relatively smooth spot in the ocean, this is the origin of the phrase, "pouring oil on troubled waters."
Winds can deform waves from a simple sinusoid. Wind the wind makes the waves too high compared to their wavelength the waves will break. In general, when a water wave becomes 1/7 as high as its wavelength, it will break.
Several waves can arrive at the same time from different directions with different wavelengths. These waves add together to create a complex pattern.
Etc
In deep water, when the wave height exceeds seven times the wavelength, the wave breaks.
Average period
To find the average period of the wave add together the periods and divide by the number of measurements.
For example I measured periods of 9 seconds, 11s,
12 s and 15 s.
The average period is (9+11+12+14)/4 = 11.5 s
the frequency is the inverse of the period or f = 1/11.5 = 0.087 cycle per second or Hz.
An equation for the wave
If we take a frozen snapshot of the wave we can write its shape as
y = A sin (2p x/L)
Notice the units of the term in parentheses, the distance units of x and L cancel out leaving a dimensionless ratio. The sine wave is defined in terms of angles such as degrees radians or grads. Scientists usually use radians. This is why the 2p appears in the parentheses, it changes the units from cycles to radians since there are 2p radians in one cycle.
Question what would you replace the 2p with if you wished to measure angles in degrees? Answer.
If instead we look at the moving wave at one position we would see it move up and down sinusoidally in time, t, the equation is:
y = A sin (2p t/T)
or in terms of frequency y =A sin (2p ft)
We can let the wave move in space and time and the equation becomes:
y = A sin 2p (x/L - t/T)
It may seem funny that we chose the minus sign here but this choice means that since L and T are positive the wave will move in the positive x direction.
Scientists often write this as
y = A sin (kx -wt)
w is called the angular frequency, instead of the number of cycles per second it is the number of radians per second and so includes within it the 2p. w = 2pf.
What is k? It has the name of wavenumber. It measures the number of radians per meter. k = 2p/L.
When scientists see a sine wave equation in space and time they look at the terms in front of the variables x and t.
They know that if they can write the equation as
y = sin a(x-vt) that the term in front of the t will be the speed of the wave.
We can change our equation to
y = sin k(x-(w/k)t)
and recognize the speed as the ratio
v = w /k
Answer You would replace the 2p radians with 360 degrees. y = A sin (360 x/L)
|
Scientific Explorations with Paul Doherty |
|
14 October 2000 |