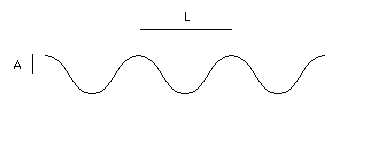
A few wavelengths of a water wave which is a sine wave with wavelength L, and amplitude A
Imagine some water waves, they are moving along with some speed C but for the moment we will freeze time and look at a still image of the waves.

Properties of this wave
The amplitude of the wave, A, is the distance in
meters between the center of the wave and its crest.
Surfers measure the wave height between the bottom of the trough and
the top of the wave. (for more on surfer measured wave heights
go
here.)The scientist's amplitude is thus
half of the surfers wave height.
The period, T, of the wave in seconds is the time between one crest and the next.
Buoys out in the ocean measure the periods of waves, the reports from these buoys can be found on the Internet. Wave heights can also be measured from spacecraft.
The wavelength, L, of the waves is the distance between adjacent wave crests.
The wavelength the speed and the period are related in the following way
L = CT
This just says that a wave travels one wavelength at a speed C during a time equal to one period.
Why is this wave called a gravity wave?
Picture a long linear pile of water magically pulled up out of the ocean and frozen in place.

Release the pile.
Gravity pulls the pile down. It falls under gravity gaining speed downward and spreading as it falls. When the crest has reached the original flat surface of the water it is traveling rapidly down, it overshoots this position and pushes down a trough in the water. The water from the original pile spreads out to both sides creating two crests each on the side of the original pile. The original wave has spread to the side. The gravitational pull of the earth and the inertia of the motion of the water both played a role in the creation of the moving wave crest. This type of water wave is called a gravity wave.
In reality waves in the ocean are not formed by magically frozen piles of water being released, they are formed when wind blows over the water. Wind creates waves which travel in one direction, not in two opposite directions.
Wave Sets
Real waves do not travel as perfect sine waves, they travel as sets of waves, sometimes multiple sets of waves overlap and add together. Let me show you a drawing of one possible simple set of six waves.

A set of six waves.
If you watch such a set moving out from the wake of a boat for example you'll see something interesting. The set of waves moves. Imagine that the set of wave shown above is moving to the right. But the individual wave crests that make up the set move within the set. If you watch real waves closely you will see that a wave is born at the back side of the set, on the left, and then moves to the right twice as fast as the whole set is moving. It grows in amplitude until it reaches the middle of the above set, then it continues to the right shrinking in amplitude and disappearing at the front end of the set.
There are thus two velocities of travel associated with a deep water wave, the velocity of an individual peak, called the phase velocity, Cp, and the velocity of sets of waves called the group velocity, Cg. In theory, for deep water waves the phase velocity is exactly twice the group velocity.
The Phase Velocity
For deep water waves the phase velocity, Cp, depends on the acceleration of gravity, g, which is about 10 m/s^2, and one wavelength of the wave, L, in meters.
Cp = (gL/2p)0.5
Taking a look at this equation we see that longer wavelength waves move faster, and that on a planet with a higher acceleration of gravity the waves would move faster.
We can express the speed in terms of the period of the wave instead of the wavelength.
Since
L = CpT
we can substitute CT for L in the above equation and find
Cp = (gCpT/2p)0.5
Solving this equation for Cp we find
Cp = gT/2p
Note that the speed is simply proportional to the period of the wave.
The Numbers
Consider a wave with a 10 second period, let's calculate its phase velocity and wavelength.
Cp = gT/2p = 9.8 * 10/ 6.28 = 16 m/s
The units of meters per second for speed result from our choice of units for g 9.8 m/s^2.
(A note on significant figures.)
and wavelength L = CpT = 160 m, over 50% longer than a football field.
A wave with 15 second period would have a speed of 23 m/s
A wave with 20 second period would have a speed of 31 m/s
In fact the phase velocity is proportional to the period and the constant of proportionality is 1.56 i.e.
Cp = 1.56 T for speed in m/s.
Surfers usually use knots for wave speeds (or sometimes miles per hour.)
To convert m/s to miles per hour simply multiply by 2.25
To convert to knots or nautical miles per hour simply multiply by 2.
So a 10 second period wave will have a deep water speed of 30 knots.
This may seem like a high speed to most surfers but when waves reaches shallower water they slow down.
How long will it take the wave to get from the buoy to me?
If there is a buoy 100 nautical miles away from your beach measuring waves with a period of 10 seconds moving toward you beach, how long will it take the waves to reach your beach?
Watch out!
Wave sets travel long distances at the group velocity of waves not the phase velocity. The group velocity which is exactly 1/2 of the phase velocity for deep water waves. Use the wrong velocity and you'll get an answer that is half as long as the real answer, you'll be the first one on the beach, but you'll have to wait a long time for the waves to arrive.
To find the time, t, for waves to travel a distance, d, at the group velocity, Cg
t = d/Cg = d/0.5 Cp
and for our example Cp = 2 * 16 = 32 knots
t = 100 nautical miles/ 16 knots = 6 hours
Notice how the factor of 2 that converts meter per second to knots is neatly canceled by the factor of 1/2 which converts phase velocity to group velocity.
Surfers in California measure the wave height between the trough in front of the wave and the crest, however surfers in Hawaii measure the height from the trough behind the wave and the crest. Since a set of waves interacting with the shore is not sinusoidal these measurements can differ, so one surfers 10 foot wave is not every surfers 10 foot wave.
I've rounded off numbers in this article to 2 significant figures.
|
Scientific Explorations with Paul Doherty |
|
7 February 2002 |