relativitytradespeedclock

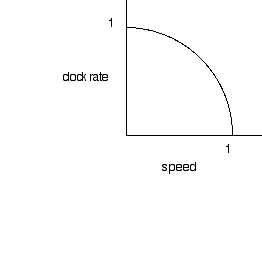
Trading speed through space for speed through time

In special relativity there is a relationship between speed and clock rate.

Speed through space changes the rate of a clock.

A high speed clock runs slower than a clock at rest.

The relationship can be shown by drawing a circular arc connecting one axis that shows speed and a perpendicular axis that shows clock rate.

If you choose a speed along the x-axis, then the arc will show you the rate at which a clock moving at that speed runs relative to you.

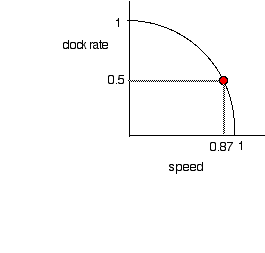
For example if you travel at a speed of 0.87 (on a scale where the speed of light is 1) Then the circle shows that your clock runs at 0.5, half speed.

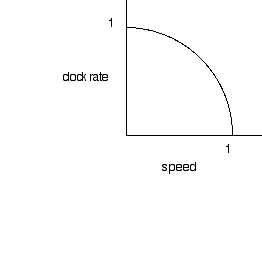
Make an interactive version of this where a visitor controls a slider to adjust the speed between 0 and 1 where 1 is the speed of light, and the clock rate goes between 0 and 1.

We can illustrate a clock actually moving at a speed that is selected, and a rate such as a heartbeat or a ticking clock for the rate of the clock running accompanied by a clock with a sweeping animated second hand.

Clock rate versus speed always falls on a circular arc.
The faster a clock moves through space the slower it goes through time.

Make a mechanical version of this exhibit where an object moves around a quarter of a circular arc.
Do this with a pivoted arm, If it is vertical a string and weight can read speed while another horizontal string reads clock rate.

We are more familiar with the concept of this trade off between speeds when we travel on a constant speed ferry and we can then trade speed to the north in space for speed to the east in space, see below.

Do the Math, here is the mathematics behind this page.

Trading east for north

Consider a ferry traveling across the San Francisco Bay, the ferry has one speed it can travel at 10 km/hr (about 6 mph)

Point the ferry east and you can cover 10 km to the east in one hour, heading to Almeda.

Point it north and you can cover 10 km to the north in one hour. Heading to Sausalito.

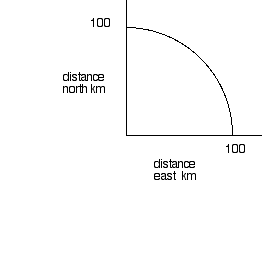
Point it northeast and you can cover 7.1 km to the east and 7.1 km to the north, toward Berkeley.

Steer a little south of northeast and you can go a little further east at the expense of going a little less far north, heading to Emeryville.

It's a sum game with the trade off of east for north given by drawing a circle of radius 10 km.

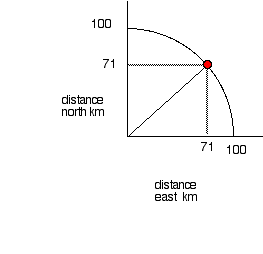
The amazing thing is that similar rules apply to speed in space and the "speed" of a clock through time, the clock rate.

Go back above.