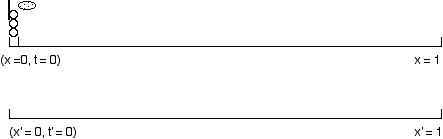
A light tennis player launches a photon of light from the baseline of his court toward the far end a light second away.
A second tennis court of identical size sits beside the first one.
The speed of light
The speed of light is defined to be exactly: c= 2.99792458 x 10^8 m/s
or about 3 * 10^8 m/s or
186,000 miles per second.
Originally, scientists defined a standard for the second which started as a pendulum clock and which recently became an atomic maser clock.
Scientists also defined a length which was the distance between two scratches on a platinum-iridium bar. However, scientists have now redefined the meter in terms of the distance light travels during a given time. The time is defined by an atomic clock.
So we have gone from a system in which we defined length and time and measured the speed of light to one in which we have defined a time interval and the speed of light and derived a distance.
Looking out in space is looking back in time.
The speed of light does make a difference when we look out at the night sky:
We see the moon as it was 1.5 seconds ago
The sun as it was 8.5 minutes ago
Saturn as it was an hour ago
Alpha Centauri as it was 4 years ago
the Andromeda Galaxy as it was 2 million years ago.
All of the above we can see with our unaided eyes.
By using radio telescopes we see
the big bang as it was 13.7 billion years ago.
I have an activity relating to this Universe City Time
Constancy of the speed of light
One of the two fundamental ideas of special relativity is that the speed of light in a vacuum is the same in every reference frame.
This seems like an innocuous statement until you realize that the speed of light coming out of an automobile at rest is c, the speed of light coming out of the headlights of an automobile in motion is c, and the speed of light coming out of a star traveling 10^6 m/s (note, a fast star was recently found traveling 6.7 * 10^5 m/s) is c both for light traveling in the same direction as the star and light traveling opposite the star. Now the idea of the constancy of the speed of light might seems strange. But it has been shown to be true by experiment.
In 1887 Michelson and Morly measured the speed of light for light traveling in the same direction as the earth in its orbit and for light traveling in the opposite direction from the earth in its orbit. Light was found to travel at c in either direction. The orbital velocity of the earth is 30 km/s = 3 * 10^5 m/s.
In 1964 Alvager measured the speed of a pulse of light emitted by a pion that was traveling at 0.99975 c in a laboratory, the light was measured to be traveling at c in the laboratory.
Relativity in your home
In a television if you have a cathode ray tube television (and not a plasma or a liquid crystal TV) the electron is accelerated in an electron gun to 1/3 of the speed of light.
Math Root
How long does it take the electron to travel the 1/3 of a meter distance from the electron gun to the screen?
The electron has a speed of v = 1 x 10^8 m/s and it travels a distance d = 1/3 meter so it takes a time, t:
t = d/v = 1/3 / 1 * 10^8 = 0.3 x 10^-8 s = 3 ns, three nanoseconds.
The time of travel of the electron must be measured by two different clocks each at rest in your reference frame. One clock measures the time the electron begins its flight and one measures the ending time. Subtract the two times to get the travel time. These clocks must be synchronized.
More on the relativistic speeds of the electrons in your television.
SLAC
Stanford Linear Accelerator Center
When the electron has traveled 10 feet along the linear accelerator it has a speed of 0.99 c and gamma is 7.09.
Where gamma measures the amount that clocks run slow or that length is contracted. Gamma = 7 means that clocks run at 1/7 the speed they do on your wrist and meter sticks are only 1/7 as long when they move past you along their length.
At the end of the linac, 3 km from the start, the speed of the electron is 0.9999999995 c and gamma is 10^5.
The rest energy of an electron is 0.511 MeV. The energy of the electron is gamma times the rest energy. So 10 feet down SLAC the energy of the electron is about 7 times its rest energy or 3.5 MeV. At the end of SLAC the energy is 10^5 times the rest energy or 50 GeV.
GPS
There are 24 satellites orbiting the earth as part of the Global Positioning Satellite navigation system.
These satellites have atomic clocks on board,
Receivers on earth use signals from these satellites to determine the location of the receiver on the earth. The satellites circle the earth twice per day at an altitude of 20,000 km and at a speed of 14,000 km/hr or 3.9 km/s or 3.9 * 10^3 m/s
Because the atomic clocks are moving relative to the surface of the earth, and because the satellites are in orbit high above the earth the clocks must be adjusted for the effects of special relativity as well as general relativity.
A moving clock appears to run slow in special relativity. The GPS satellites are orbiting at a speed that is fast enough to make the clock lose 7,000 nanoseconds a day. This would lead to an error in the location of the receiver on the ground of 7000 feet or about 1.5 miles per day.
A moving clock appears to run fast when it is in a lower gravity environment. The clocks run fast so that they gain about 45,000 nanoseconds a day due to general relativity. The combination of the gain from general relativity and the loss for special relativity would create an error of about 38,000 ns or 7 miles per day if corrections were not made.
The first GPS satellite was launched without the
relativity correction program operating. The data showed that
Einstein's theories predicted the changing clock rates of the GPS
satellites within the errors of the measurements. The engineers then
turned on the correction program.
Twin Paradox
The clock on a spaceship moving fast runs slower than a clock at rest.
As it passes beside you at the origin (no classical doppler shift)
You see your twin take a spaceship ride covering 10 light-years at 0.87 c taking 11.5 years.
On the way out your twin's clock seems to run at 1/2 speed, also on the way back.
So you see her clock tick off ( 2 * 11.5)/2 years or 11.5 years while you age 23 years.
Paradox because she sees your clock run at half speed too. (But she turns around) the turn around is the key to understanding the paradox.
E = mc^2
The power of:
The sun.
Nuclear reactors
Nuclear fission and fusion bombs.
Speed of light
Consider an extra long tennis court. It is 50 meters long.
Tennis players serve the ball at 50 m/s, it takes one second for the ball to cross the court.
A second tennis court is mounted on a truck driving beside the first tennis court at 25 m/s.
The tennis player, named Zeno, standing on the first court serves the ball onto the moving tennis court just as the two tennis courts exactly line up.
We can all figure out what happens.
The server and the observer on the moving tennis court both agree it takes 2 seconds for the ball to cross the 50 m long moving court. they each have a slightly different interpretation of the events.
A viewer on the moving tennis court sees the ball traveling 25 m/s across the 50 m long court. It takes 2 seconds for the ball to cross the court.
Meanwhile the server on the ground sees the ball traveling 50 m/s but the far end of the tennis court is a moving target, after one second the end of the moving court has traveled 25 m. The ball strikes the end of the moving court after 2 seconds when the court has moved a total of 50 m the ball has traveled 50 m.
The above is known as Galilean relativity.
At high speeds things get strange.
Consider light tennis.
Two identical tennis courts are constructed. They are 300 million meters long, 1 light second.

Now allow the second, prime, tennis court to move at 87% the speed of light, v = 0.87 c.
Both tennis courts line up so that the server that sends out the flash of light is at the same baseline location on both courts. (The light flash starts at x = 0 and t = 0 and at x' = 0 and t' = 0)
On the court that is stationary the light takes 1 second to travel the 300 million meters across the court, It arrives at the far end at x = 1 (light second) and t = 1 second, where c = x/t = 1, in these units where distance is measured in light seconds the speed of light is 1 light second per second.)
The amazing thing is that an observer on the moving court sees that it takes the light a second to cross the moving court as well.
The speed of light is the same in all reference frames.

The two views of the server and the moving observer are now quite different.
Lengths and clocks don't behave like they do around the house.
The observer on the moving tennis court sees a flash of light travel the 300 million meter or 1 light second length of the tennis court in 1 second, at c, the speed of light.
Event 1 the light flash leaves x=0 at t=0.
In the moving tennis court frame, the prime frame, the light leaves at x' = 0 and t'=0 it is still event 1.
The light arrives at the end of the tennis court in the stationary frame at
event 2 x = 1 and t = 1.
The light arrives at the end of the moving frame at
event 3 x' = 1 and t'=1.
An observer in the stationary frame sees event 3 happen
at x = 3.8 and at t = 3.8
The viewer sees the moving tennis court only 1/2 as long due to length contraction, by the time the light has reached the end of the stationary tennis court the seemingly short moving court has moved on.
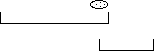
By the time the light reaches the end of the stationary tennis court the end of the moving court has moved on.
![]()
The light eventually catches the end of the moving court at position
x = 3.8 and time = 3.8
so that the speed the observer sees in the moving frame is c = x/t = 3.8/3.8 = 1
The light travels at the speed of light.
We can check the answer, the light starts at time 0 and at x = 0 while the end of the moving court starts at time 0 at x = 0.5 moving at v = 0.87 c
The two meet when t = 0.5 + 0.87 t or when t = 0.5/0.13 = 3.7 s at which time the light has traveled to x = 3.7 light seconds.
The observer in the moving frame sees event 2
at x' = 0.26 and t' = 0.26
The frame of the light server seems to be moving leftward at 0.87 c, it is also length contracted to half its original rest length. The light pulse is seen to arrive at the end of the court after only t' = 0.26 s having moved only x' = 0.26 light seconds of distance.
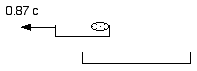
so that the speed the moving observer sees in the stationary frame is c = x'/t' = 0.26/0.26 = 1
Everyone agrees that their measurement of length and time in moving frames change to keep the speed of light a constant.
To calculate these events as viewed in a different frame I used a Lorentz transformation.
The Lorentz transformation of an event at position x and time t in one stationary frame to another frame moving at speed v in the x-direction, i.e. to an event at position x' and time t' is
x' = g (x - vt), t' = g (t - vx/c^2)
where g = 1/(1-v^2/c^2)^0.5
and from the moving frame to the stationary frame
x = g (x' + vt'), t = g (t' + vx'/c^2)
What you might expect if you didn't know relativity.
The photon leaves the origin of both frames traveling at the speed of light.
In the rest frame it reaches the end of the court after 1 second traveling 1 light second in distance at a speed of light = 1.
However, the moving frame end has moved on. It started at time = 0 at x = 1 and then moved at a speed v = 0.87 c.
The light reaches the end of the moving court when c t = 1 + 0.87 ct with c=1
the light reaches the end at t = 7.5 s.
You would expect a person in the moving frame to see the light cover the distance of 1 in 7.5 s for a speed of 1/7.5 = 0.13 c.
This is not what happens. You actually see the length of the moving court shrink to 1/2 its rest length and you also see clocks in the moving frame run slower so that as shown above the speed of light in the moving frame is actually 1.
Magnetism
Is just electricity viewed in a moving frame of reference.
Paul's Relativistic
spaceship views.
Examples of time changes
Muon
jet flight, 1971 707
satellite GPS
|
Scientific Explorations with Paul Doherty |
|
15 April 2005 |