Introduction
Hold a slinky between your hands, model transverse wave resonances as well as longitudinal wave resonances. Learn about nodes and antinodes of motion and compression.

Material
A slinky
about 3 meters of 20 pound test monofilament fishing line
2 chairs
Optional substitute for nylon line, a length of 1/2 inch PVC pipe
masking tape

Assembly
Tie the fishing line to a chair. After the first experiment described below slide the slinky onto the fishing line then tie the other end of the fishing line to another chair. Pull the chairs apart until the line is taut.

A tightly stretched monofilament line supports a slinky. Compressional waves are easily seen.

Optional,Thread the slinky onto a length of 1/2 inch PVC pipe. Place the pipe between two tables or clamp one end to a table.

To Do and Notice
Hold the slinky between your hands. The slinky will be horizontal and sag.
Move both of your hands up-and down together. Find the lowest frequency which produces the largest motion of the slinky for the smallest motion of your hands. (About one cycle per second.) One large hump, half-a-wave should appear moving up and down on the slinky.
Count the rhythm every time the middle of the slinky hits bottom, 1,2,3,4,1,2,3,4,...



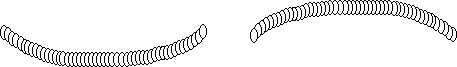
Notice that the center of the slinky moves up and down the most and your hands the least.

Move your hands in opposite directions, that is, move the right hand up when the left hand moves down and vice-versa. Move them in the same rhythm as above. Notice that your hands move a large distance whole the center of the slinky hardly moves at all. If you have trouble, try this on a tabletop.



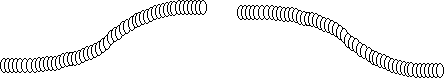
Count the rhythm every time your right hand hits bottom, 1,2,3,4,1,2,3,4,...

What’s Going On?
When you move your hands together you make a half-a-wave on the slinky the middle of the slinky is an antinode, a point of maximum motion while the handheld ends are nearly nodes, points of no motion.

When you move your hands opposite, a half-a-wave also fits on the slinky. However, this half wave has one node in the center and two antinodes near the handheld ends.

The timing on both of these is the same, that is, the period is the same. They both are resonances in which one-half-wave fits onto the slinky.

Both of these patterns of motion have the fundamental frequency of oscillation, the lowest frequency of motion for a slinky held at both ends. It is close to 1 hertz.

Etc.
For the transverse motion of the slinky, at places where the motion of the slinky passes through zero, a node of motion, the slope of the slinky changes the most, an antinode of slope. So at the same places where there are nodes of motion, there are antinodes of slope.

Longitudinal Waves
To Do and Notice
Thread the slinky onto the monofilament line as described under assembly.

Grab the ends of the slinky in your hands.
Stretch the slinky to between 1 and 2 meters long.

Move your hands together and then apart, just as if you were clapping. Notice the motion of the slinky. Your hands move a lot while the center of the slinky moves very little. The center is a node.
You can attach a small flag of masking tape to the center of the slinky to make it easier to see that the center is not moving.



Next notice the spacing between the slinks (turns) of the slinky. When the slinks are jammed close together the slinky models high pressures in a gas, where the atoms are closer together. When the slinks are far apart , the slinky models low pressure in a gas. Let’s call closely spaced slinks high pressure and widely spaced slinks low pressure.
Notice that the pressure change is greatest at the center where the slinks alternately bunch-up and spread apart, and where the side to side motion of the flag is the least.
Count the rhythm of this motion: 1,2,3,4,1,2,3,4,...

Move both hands in the same direction, if the slinky stretches right-left move both hands to the left then to the right. (One of our teachers described this as the sound of one hand clapping twice.)


Notice the motion of the slinky which is called longitudinal motion. Find the frequency of hand motion that produces the largest motion of the center of the slinky for the smallest motion of your hands.
Count the rhythm of this motion: 1,2,3,4,1,2,3,4,...
Notice that the center of the slinky is an antinode, your hands are nearly nodes. The flag marking the center whips back-and-forth.
Notice that in the center the slinky moves back and forth but the spacing between the slinks near the center does not change. The center is an antinode of motion but a node ( a place with no change) of pressure.
At the nodes of motion near your hands however the slinks bunch together and then spread apart: the pressure changes a lot. The handheld ends are antinodes of pressure.
Notice also that when one hand is at high pressure the other is low. The ends then swap. The high pressure hand becomes a low pressure and vice-versa. In other words, the slinks bunch up near one hand while they spread out at the other.

What’s Going On?

When your hands move together one-half-wave of longitudinal motion fits on the slinky. This is the lowest frequency resonance of the slinky held at both ends, it is called the fundamental frequency.

When your hands move opposite, one-half-wave of longitudinal motion also fits on the slinky but this time the node is in the middle while your hands are near antinodes.

A sound wave is a longitudinal wave. A sound wave can be viewed either as a wave of motion of atoms or as a wave of pressure. In a standing sound wave in a tube nodes of motion occur at the same place as antinodes of pressure. When both of your hands move together and apart as in a normal clap you are modeling sound waves in a tube closed at both ends. There are motion nodes at the ends and pressure antinodes. When you move both hands in the same direction, the non-clap, you are modeling a tube open at both ends. It has motion antinodes at the ends and pressure nodes.

To Do and Notice

Find a higher frequency resonance of the longitudinal wave in which you move both hands in the same direction (anti-clap). You should have to move your hands about twice as often as in the lowest frequency resonance you created before.



Count the frequency: 1,2,3,4,1,2,3,4
Notice the motion of the slinky, there are two nodes each about 1/4 of the way from each end. Mark the nodes with flags of masking tape.
One full wave fits on the slinky.
When there is a high pressure near one node there is low pressure near the other. The high pressure and low pressure regions switch positions each cycle.

Move your hands opposite each other (clap) and find the next higher resonant frequency.


nodes | | |

There will be three nodes on the slinky, one in the center and the other two 1/6 of the slinky from each end.
3/2 of a wave fits on the slinky.
Notice the pressure changes on the slinky, when one node is experiencing high pressure the adjacent one experiences low pressure.
With time, each node oscillates from high pressure to low and back again.

What’s Going On?
High pressure and low pressure nodes alternate in time as well as in space.
To create an odd number of nodes move your hands opposite each other, clap hands.
To create an even number of nodes move your hands in the same direction.

Etc.

In the Exploratorium sound column a tall cement tube closed at both ends you can create a standing sound wave by playing an aluminum bar tuned to be in resonance with the column. When you place your ear at the floor, at a node of motion, the sound is loud, when you raise your ear to an antinode of motion the sound just about disappears.
This shows that your ear detects pressure changes. The floor is an antinode of pressure change.

Teaching tip.

Store slinkies in a ziploc bag to keep them from mating.

You can also hang a slinky from two cords, called a "Bifilar suspension" to make it show longitudinal waves.
Return to Day 10