
Introduction
Consider the interference of light coming through two slits. Use geometry to calculate the angle on a distant screen of maxima and minima of light intensity.
To Do and Notice
Look at this figure.

Light passes through two very narrow slits and hits a distant wall creating an interference pattern.
where the distance between the slits is d, and the distance to the wall is L.
The light has a wavelength l .
Does the light interfere constructively or destructively at an angle q?
To find out whether there is constructive or destructive interference, knowing that light starts out at the slits in the same phase, we need to know the difference in the distance to the wall from each of the slits.
Use the following diagram:
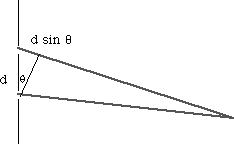
The extra distance traveled by the light going through the top slit is d sin q.
Where are the maxima?
The extra distance traveled by light from the top slit to the wall is d sin q.
When q = 0 the distance from each slit to the wall is the same and the waves arrive in phase to create a maximum.
The first maximum to the side is located at an angle where the path length difference is one complete wavelength:
for small angles l = d sin q = d q
or q = l / d
The next maximum occurs at a path length difference of 2 l. and so on.
The maxima are regularly spaced at an angular separation of q.
Geometry and approximations.
d is the hypotenuse of a right angle triangle I have constructed. The side of the right angle triangle opposite angle q is of length d sin q and is the extra distance traveled.
The lines from the top slit to the wall and from the bottom slit to the wall are very nearly parallel since the distance between the slits is about one wavelength of light and the distance to the wall is several meters. The angle between the lines in radians is given by the ratio of these distances. 5 x 10-7m/5m = 10-7 radians.
Since the lines from the slit wall to the screen are very nearly parallel we can use the following construction:
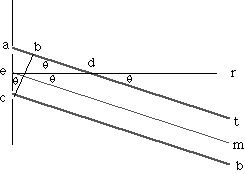
The angle between lines em and er is defined to be q.
Lines em and at are parallel. Line er crosses lines em and at.
Therefore the angle between lines er and at is also q.
Triangle ade is a right triangle. The angle ead is 90-q.
Triangle abc is a right triangle, it also contains angle ead.
Therefore angle acb is equal to q.
|
Scientific Explorations with Paul Doherty |
|
24 May 2000 |