Introduction

A spinning rod with a mark near one end is set rotating and spinning at the same time. Amidst the blur of the spinning cylinder, the mark appears three times, forming a stationary triangle. Finding out why the spinning cylinder creates this pattern is an excellent activity for scientific inquiry.

Material

• A few feet of 3/4 inch PVC tubing (note the 3/4 inch refers to the inside diameter)
• A PVC tubing cutter, or hacksaw.
• Masking tape, 3/4" wide
• colored felt tip pens (Non Permanent)
• A hard smooth surface

Assembly

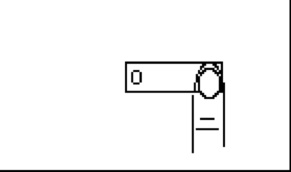
Cut a tube to a length 3 times its outside diameter. The outside diameter of the PVC named above is 1 inch, so cut a 3 inch long cylinder.

Make an X mark at one end of the cylinder and an O mark on the other end.

Have more PVC available to be measured and cut to other lengths as you experiment.

To Do and Notice

Place a finger on the X and press down launching the cylinder so that it spins and rotates at the same time.

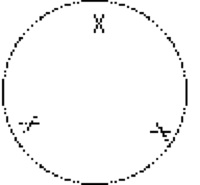
Notice that the spinning cylinder stabilizes so that the X appears at the vertices of a triangle.
Notice the O does not appear.

Next place your finger on the O and spin the rod.
Notice that the O forms a triangle while the X does not appear.

Do experiments to figure out what is going on.
Suggestions:
Make several markings on one end.
Look at the spinning rod from underneath through a transparent table.
Look at the spinning rod in sunlight (which does not strobe on and off like fluorescent lights.)
Try cylinders of different lengths, notice the different stable patterns.
Notice that the center of the spinning cylinder is above the table, the cylinder rotates with one end in contact with the table surface.
File or cut a notch in one end of the cylinder. When the notch rotates it will tap on the table. Which end do you launch to produce the tapping.

What’s Going On?

Don't read this section below until you have done some experiments yourself.

When you launch the rod it spins about its long axis and rotates about a line perpendicular to this axis.

Looked at from above. As the rod spins the top of one end moves in the direction of rotation while the other end moves opposite to the direction of rotation.
The arrows in the image show the direction of motion of the ends of the tube and the direction of motion of the top surface.

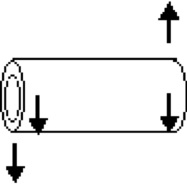
The speed of the end of the tube due to rotation about a vertical axis is equal in magnitude to the speed of the end due to spinning.

At one end the two velocities add so the mark on that end is moving so fast it is a blur to the eye. At the other end the velocities are equal and opposite so the mark comes to rest for a moment and can be seen by the eye.

Since we see 3 markings around the blurred circle we know that the cylinder is making 3 spins for every rotation.

This is due to the fact that the cylinder is rolling without slipping on the table surface.

Math Root

The circumference of the circle, C, that the end moves through as it goes around its blurry circle is pi times the length of the cylinder, L.
C = pi L

The circumference of the cylinder, c, is pi times its diameter.
c = pi d

If it rolls without slipping the cylinder must roll three diameters while the end goes around in one complete circle.

C = pi L = 3 pi d = 3c

So the number of times that the cylinder spins in one rotation is
C/c = 3.
This is why there are 3 markings!

Going Further

Here are some engineering challenges once you have figured out the science of the rotating cylinder.

Cut the cylinder to a length so it makes a pattern of 4 markings? How about 2.

Re-mark the original cylinder, that makes a triangular pattern, so that it makes a pattern of 6 markings.

Etc

It may be easier to launch the cylinder in a paper plate or a pizza plate with a gently upcurved edge.

Engineering practices in the Next Generation Science Standards can be investigated using falling dominoes.

1. Asking questions and Defining Problems: First ask the scientific question of why is there a triangle, then when you understand this return to define the engineering problem which may be to make a cylinder that spins with 4, or even 2 or 5 marks in a stationary pattern.
2. Developing and using models: Observe the motion of the cylinder closely, then create a mental model for what is happening.
3. Planning and Carrying out investigations: Using your model cut some new cylinders, try different lengths perhaps.
4. Analyze and interpret data: Measure the diameter of the cylinders and their lengths.
5. Using Mathematics and computational thinking: Compare the ratio of length to diameter for each cylinder that makes a stationary pattern.
6. Design Solutions: Design a cylinder that will meet the engineering challenge.
7. Engaging in Argument from evidence: Spin your cylinder and discuss how the predicted result agreed with or disagreed with your expectations.
8. Evaluate and Communicate information: Compare your solution with other engineering teams, and write a final report on your solution.