A Modern Refracting Telescope
A telescope makes an image of the extremely distant star on the axis at the focal point.
The eyepiece is placed so that its focal point is coincident with the focal point of the objective lens.
In this configuration parallel light comes into the telescope and parallel light exits the telescope.
This parallel light enters and eye and the person sees a star.
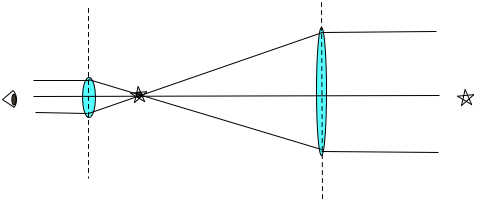
A distant star sends parallel light into the Galileoscope.
The objective lens makes an image of this star at its focal point, a distance of fo from the center of the lens.
The eyepiece lens is placed so that its focal point is at the position of the image of the star.
Light rays exit the eyepiece lens parallel.
Do your own ray tracing.
The chief ray goes straight through the center of both lenses.
Parallel rays entering the objective lens bend and come together at the focal point.
They become focal rays which exit the eyepiece lens parallel.
The f number
Notice that the light that enters the large diameter objective is condensed as it exits the eyepiece. A telescope is a light collector.
We usually express the light gathering ability of a lens by its fnumber which is the ratio of a lens focal length to its diameter.
The Galileo scope objective has a focal length of fo =50 cm, and a diameter of do= 5 cm.
This gives it an fnumber ,
f# = fo/do = 10.
The f number controls the exposure time for film or digital light sensors. Smaller fnumbers have larger light collecting abilities. Light collector is proportional to the area of the lens and so it is proportional to the square of the diameter. If you double the diameter of a lens, and so cut the the fnumber in half the light collecting ability quadruples and the exposure time is cut to a quarter. A lens with a small fnumber is called a "fast" lens.
Telescopes with fnumbers under 10 are usually made with more expensive aspherical lenses.
Telescopes also are magnifiers, but what to they magnify?
Look at an off axis star.
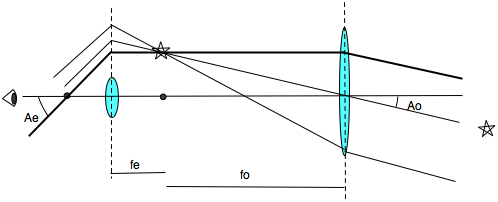
Starlight enters the objective lens with an angle Ao from the lens axis.
Follow the ray trace on the uppermost, darker ray, this is the focal ray of the objective lens.
The focal ray exits the objective lens parallel to the axis. Also follow the chief ray that goes straight through the center of the objective lens.
Where these two rays meet there will be a real image of the star. This real image is in the focal plane of the objective lens and in the focal plane of the eyepiece lens too.
Keep following the dark ray, it is a parallel ray for the eyepiece lens and bends so as to pass through the focus of the eyepiece lens.
The exiting rays are all parallel, and make a larger angle Ae with respect to the axis of the telescope.
Note, to understand all of this, you need to know how ray tracing works, the rays we use to find the path of light don't actually hit the eyepiece lens, they bend at the dotted line extension of the centerline of the eyepiece lens. The light that does hit the eyepiece exits parallel to these rays. I drew this diagram like this on purpose just to make this point about ray tracing.
The magnification of a simple telescope, m, is Ae/Ao which by simple geometry is seen to be the ratio of the focal lengths of the objective, fo, divided by the focal length of the eyepiece,
fe = 2cm.
m = fo/fe = 50/2 = 25.
Consider one star on the axis of a telescope and a second star off axis, parallel light comes from both stars one parallel to the axis one at an angle of Ao . Perhaps the stars are separated by 1/5 of a degree, barely visible as two separate stars as are Mizar and Alcor the two stars that make a pair that is the middle "star" of the three stars that make up the handle of the big dipper.

The middle star in the handle of the big dipper is a double star. Mizar and Alcor, often used as an eye test.
The Galileo scope at 25 power magnification will increase the angular separation of 1/5 of a degree between Mizar and Alcor to 5 degrees. The telescope magnifies angular size.
A telescope magnifies the angle between a star on the axis and a star off the axis. Alpha eye, Ae, is larger than Alpha objective, Ao, by the magnification.
It is a simple exercise in trigonometry to derive the equation for magnification based on the focal lengths of the lenses.
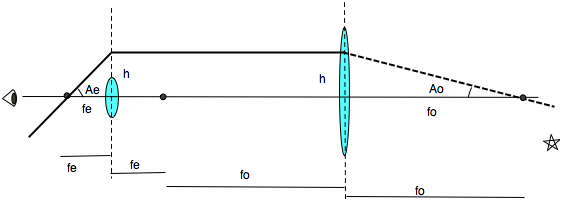
To derive the magnification of the Galileoscope, note that h = fo tan Ao = fe tan Ae.
For small angles when A is measured in radians, tan A = A so we have fo * Ao = fe * Ae
and Ae/Ao = fo/fe
Note that a star below the axis appears above the axis, so this telescope inverts the image top to bottom and right to left.
Field of View
At 25 power the Galileoscope has a field of view of 1.5 degrees. The moon will fit across the field of view 3 times because the moon subtends 0.5 degrees of arc.
At 50 power the field of view is 1/2 as wide, 0.75 degree, and the moon fills the telescope field.
The rotation of the earth moves the moon out of the field of view of the telescope in 2 minutes.
Resolution
The resolution of a telescope, the smallest angle between two stars that it can resolve, is A = L/D where L= 5 x 10^-7 m is the wavelength of light, and D = 5 cm is the diameter of the objective lens, and where angle is in radians. So the angle is 10^-5 radians. Converting to arcseconds this is about 2.5 arcseconds.( 1 radian = 57.3 degrees = 206,000 arcseconds)
Galileo's Telescope
Galileo's telescope used a converging or convex lens for the objective lens, and a diverging lens for the eyepiece.
Once again the telescope was made so that the focal points of both lenses coincided.
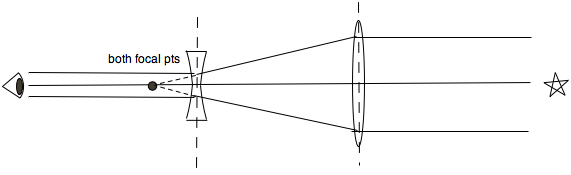
As a test see if you can follow the ray tracing from the parallel light in from the distant star.
The Chief ray runs along the axis of both lenses. The parallel rays are bent by the objective lens so as to come together at the focal point.
Rays converging at the focal point of the eyepiece lens (a negative or diverging lens) come out parallel.
Let's now look at the magnification of the Galileo telescope by looking at an off axis star.
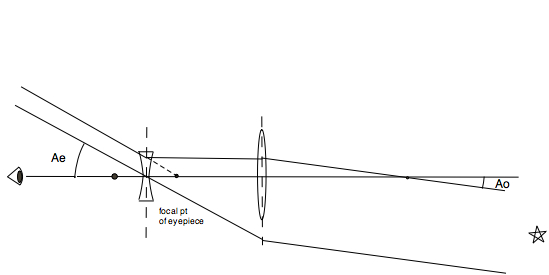
This requires a much trickier ray tracing.
Light from the distant star enters the objective lens parallel, making an angle Ao with the axis of the lens.
The focal ray goes through the focal point of the objective lens and emerges parallel to the axis and then hits the eyepiece lens.
It exits the eyepiece as if it radiated from a focal point of the eyepiece lens (dotted line).
Since both lenses have their focal points at the same place we know the light rays exit parallel to each other, so we can draw the chief ray for the eyepiece lens which makes an angle Ae with the axis.The ration of Ae/Ao is the magnification of the telescope.
Simple trigonometry as above shows that m = Ae/Ao = fo/fe
where fo is the focal length of the objective and fe is the focal length of the eyepiece.
Thus by having a long focal length objective and a short focal length eyepiece the telescope gave the observer a magnified view.
Note also that objects below the axis appeared below the axis to the observer....this telescope does not invert images.
Combining Lenses
When you place two lenses much closer together than their focal length you can treat them as one lens with a new focal length
A lens with a focal length f1
placed near a lens with a focal length f2
behaves like one lens with a focal length F where 1/F = 1/f1 + 1/f2
Remember that concave lenses have negative focal lengths.
The power of a lens is often measured in diopters, D.
The power of the lens is D = 1/f when f is the focal length measured in meters.
A 1 diopter lens has a focal length of 1 meter
a 2 diopter lens has a focal length of 1/2 m.
To find the power of two lenses in diopters simply sum their individual powers.
D = D1 + D2
In the eyepiece of the Galileoscope two achromatic lenses of focal length 4 cm = 0.04 m are combined to make one eyepiece with focal length
1/F = 1/0.04 + 1/0.04 = 1.0,02 so F = 0.02 cm
done with diopters this becomes D = D1 + D2
D = 25 + 25 = 50 so that F = 0.02 m
Achromats
The objective lens is an achromat. It brings red and blue light to the same focal point.
Newton claimed it would be impossible to make a refracting telescope that would bring different colors of light to the same focus.
A single convex lens has chromatic aberration. The glass has a different index of refraction for each color of light, so each color is refracted by a different amount by the lens. The changing index of refraction as a function of wavelength is called the dispersion of the glass. Glass refracts blue light more than red light.
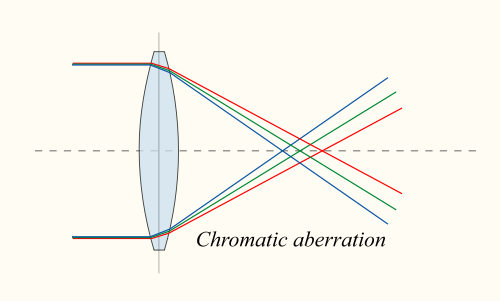
A double concave lens will focus different colors of light at different distances. This is called chromatic aberration.(You need to view this image on the website to see the colors.)
For crown glass the index of refraction is near 1.5 and varies with wavelength as shown in this table:
red 640 nm n = 1.509
green 500 nm n = 1.515
blue 486 nm n = 1.517
Flint glass has an index of refraction near n = 1.65 which also varies as wavelength.
red 640 nm n = 1.62
green 500 nm n = 1.64
blue 450 nm n = 1.65
In the mid 1700's an englishman, Chester Moore Hall, realized he could combine a double convex lens of crown glass with a plano-concave negative lens made of flint glass to reduce chromatic aberration. Crown glass has low dispersion while flint glass has high dispersion. Each of the lenses has a different index of refraction. The two lenses can be combined to make a lens which focuses both red and blue light (but not green light) at the same focal point. The lenses in the Galileoscope are made so that they have the same radius of curvature and fit together well.
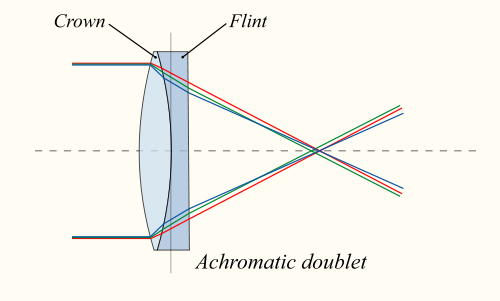
A doublet lens made of crown and flint glass can focus red and blue light at the same point.(The web page illustrates this in color.)
Barlow lens
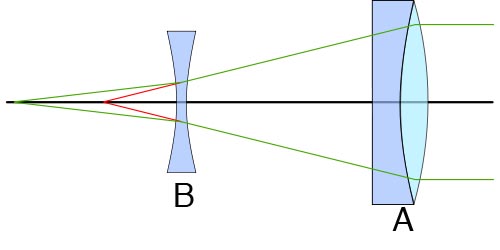
An objective lens, A, brings parallel light to a focus as indicated by the red lines. Lens B is a Barlow lens, a negative lens that diverges the light slightly bringing it to a focus as shown by the green lines. The focal length of the combination of lenses is longer than that of the original objective lens. If the angle at which the green lines converge is half the angle of the red lines then the magnification of the telescope will be doubled. Here the objective lens is achromatic, made of a combination of two lenses made of different materials.
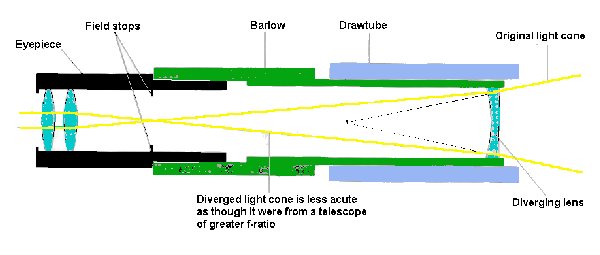
The eyepiece "lens" is made of two lenses. The Barlow lens at the right makes the focus of the Barlow/objective lens at the focal point of the eyepiece lenses.
Going Further
Tripod source
J & R Music / Computer World www.jr.com
Phone: 800.426.6027
Model: DAS TRAVLRV - VISTA PHOT (Davis & Sanford TRAVLRV Tripod)
Price: $14.99 + shipping (which worked out to $1.20 per unit - Note: we did
order 115 units)
Other tips:
- buy a white paint pen and mark the focus (tube length) for EACH
eyepiece. Otherwise, it's a real bear and wastes time.
- there's a nice hack to turn a standard 3' poster tube into a
carrying/storage case. Put some moldable/cut-able foam/felt into both
end caps...use bubble wrap to wrap the extra eyepiece...and you've got
a nice sturdy case.
The main Galileoscope website: https://www.galileoscope.org/gs/
Teaching with the Galileoscope http://www.uwyo.edu/caper/info.asp?p=16091
Laboratory exploring Galileoscope optics http://www.waiferx.com/Physics/2009/Fall/Astr210L/Labs/In-class/TelPow.pdf