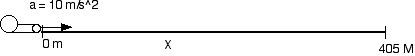
CSET 2
Physics
Kinematics Problems
Motion in a straight line.
The first step in any kinematics problem is to draw the problem.
Put values in your drawing for everything you know, like the initial position of an object and its initial velocity.
Then label the thing you are asked to find like the final position.
For example, A dragster starts from rest and accelerates at 10 m/s^2 for 405 m. How long does it take the dragster to cover 405 m?
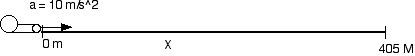
t = ?
See below for the solution. This is a problem of constant acceleration.
Basically kinematics problems come in two types:
constant velocity
and
constant acceleration.
Constant Velocity
This is the simplest kind of problem and we solve it in our cars every day.
There is basically one equation
x = xi + v * t
Where x is the final position, xi, is the initial position (usually 0) v is the velocity and t is the time.
For example: A turtle travels at 0.5 meters per second for 100 meters how long does it take?Draw it first
x = xi + v * t
100 = 0 + 0.5 * t
solve for t get t = 100/0.5 = 200 s
Constant Acceleration
There are three basic equations for constant acceleration, a.
(Note the constant acceleration is often the acceleration of gravity g = 9.8 m/s^2.)
The first one gives velocity versus time.
vf = vi + a * t
Where vi is the initial velocity, vf is the final velocity, and t is the time.
The second gives position versus time.
xf = xi + vi*t + 1/2 a * t^2
where xi is the initial position, vi is the initial velocity, and xf is the final position.
The third equation gives the velocity versus position.
vf^2 = vi^2 +2 a * (xf - xi)
Where vf is the final velocity, vi is the initial velocity xf is the final position, and xi is the initial position.
The dragster problem is one with constant acceleration over a known distance where we want the time it takes to cover the distance. Looking at our three choices of equation we could use we use the second one
.xf = xi + vi*t + 1/2 a * t^2
405 = 0 + 0 * t + 1/2 10 t^2
405 = 5 t^2
t^2 = 81
t = 9 s
Rule of thumb. Solve for the time.
"Time, gentlemen, time." Quote by a British bartender.
"Does anybody know what time it is?" lyric
In any kinematics i.e. motion problem, if the problem does not give you the time, then solve for the time at which the final result happens.
Once you know the time, plug it into the correct equation to get what you want.
A Shortcut using energy
If all the problem wants is speed for an object moving under gravity near the surface of the earth conservation of energy can be used to solve the problem.
The kinetic energy of a moving object of mass m and speed v is Ek =1/2 mv^2
The potential energy at height h where g is the acceleration of gravity is U = mgh
Set the initial energy equal to the final energy to get
Eki + Ui = Ekf + Uf
1/2 mvi^2 + mghi = 1/2 mvf^2 + mghf
A body is thrown straight up from the surface with a speed 10 m/s how fast is it going when it is 2 meters above the surface? The acceleration of gravity is g = 10 m/s^2.
Draw it!
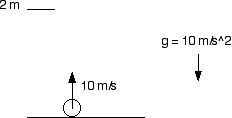
1/2 mvi^2 + mghi = 1/2 mvf^2 + mghf
1/2 m 10^2 + 0 = 1/2 mvf^2 + mg2
Divide out all the m's they don't matter
50 = 1/2 vf^2 + 2 * 10
60 = vf^2
vf = 7.75 s
Note that in the equation for energy the fact that g is downward and so often a negative quantity has already been taken into account in the potential energy equation so g is a positive number in the term mgh.
|
Scientific Explorations with Paul Doherty |
|
10 October 2005 |