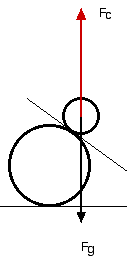
Forces

In a physics problem with forces always start by drawing a force isolation diagram.

Pick an object then draw all the forces on that object.

Assume an object like a sphere of steel with a mass, m.

The forces usually encountered in physics problems.

Gravity

Near a planet there will be a force of gravity on the object.

The force is toward the center of the planet.

Near the surface the force is constant, near the earth the constant force is F = mg

where g is the constant of proportionality between mass and force.

since F = ma and F = mg then ma = mg and a=g

so the constant of proportionality is the acceleration of gravity near the surface of the earth.

The force of gravity acts as if it applied at one point on the object, called the center of gravity (near the surface of the earth where the force of gravity is constant, the center of gravity is at the center of mass. For very large objects where gravity changes with distance the center of gravity is not the center of mass.

Farther from the surface F = GMm/r^2

where G is the universal gravitational constant, M is the large mass of the planet, m is the mass of our object, and r is the distance between the centers of the objects.

(R as the distance between centers is important, it is strictly true only for spheres by it works pretty well for non-spheres as long as they are much smaller than the earth.)

Spring Force

A spring exerts a force if it is compressed from its rest length or stretched from its rest length.

If a spring is compressed or stretched a distance x then the force it exerts is

F = - k x

where k is a constant of proportionality called the spring force.

The force is opposite the direction of the motion so there is a negative in this equation.

Contact Forces

When two bodies touch each other they exert forces on each other.

These forces are due to electrical interactions between the atoms making up the objects.

There is no fundamental equation for contact forces.

The contact forces are divided into two pieces. A piece that is perpendicular to the plane tangent to the two objects at the point of contact called the normal force F_N

And a force parallel to the tangent plane called the friction force F_f

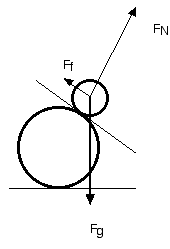
The vector sum of the normal force and the friction force is the contact force.

There are two kinds of friction forces static and dynamic.

Dynamic friction occurs when an object is sliding across another object.

Static friction when the an object is not sliding.

The equation for the dynamic friction force F_f is F_f = m F_N

So if a crate weighing 10 N is sliding across the ground with a coefficient of sliding friction of m = 0.3 then the dynamic friction force is

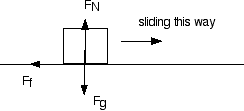
F_f = m F_N

F_f = 0.3 * 10

F_f = 3 N

It's more complicated for static friction.

F_f < = m F_N

The static friction force is less than or equal to the friction coefficient times the normal force.

This is probably the first time students will encounter an equation with a less than or equal to sign in it.

How hard must you push on a crate weighing 10 N sitting on a floor with a coefficient of static friction of 0.5 to get it to start moving?

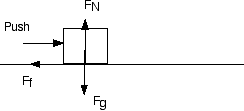
F_f < = m F_N

F_f < = 0.5 * 10

F_f < = 5 N

So the maximum static friction force is 5 N, you must push the box harder than 5 N to exceed the static friction force and make the box start to slide.

Note that in a problem the static friction force can have any value from 0 to its maximum value.

Tension

Strings exert a tension force on objects.

The tension force exerted on the object by the string is in the direction of the string.

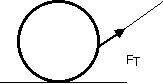
There is no equation for the tension force.

Scientific Explorations with Paul Doherty

© 2005

10 October 2005