resolution

Resolution

A Math Root

Consider two identical black bars separated from each other by their width.

What is the angular width of the central white bar that allows a human eye to see that there are 2 separate black bars?

We use the angular width because whether the eye can see two bars or not depends not only on the distance between the bars, s, but also the distance to the bars from the eye, D.

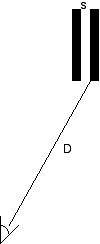
The white space between two black bars has width s and is located a distance D from an eye.

The angle in radians, A, subtended by the distance s at a distance D is approximately

A = s/D for small values of s/D

For example a 1 cm white bar 1 meter away subtends an angle of A = 1/100 = 0.01 radians.

Now, there are 2pi radians in a complete circle and 360 degrees so

360 degrees/2pi radians = 57.2 degrees per radian.

Thus, an angle of 0.01 radian is about 0.57 degrees.

(Optional, for larger values of s/D, A = 2 arctan(s/2D) so stick to small values!)

So What?

A human eye with 20/20 vision can see bars separated by an angle of 1/60 degree also known as one arcminute or 0.3 milliradian, 3 x 10^-4 radian.

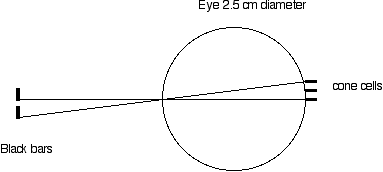
An eye vieweing black bars. The images fall on cones on the retina. The lines cross at the center of the "lens" that is composed of the cornea and lens of the eye.

The light receptors known as cones in the center of the retina, on the fovea, have a width of 2.5 micrometers, 2.5 x 10^-6 m. The eye is about 2.5 cm long. From the front of the eye, one cone subtends 0.1 milliradian. A = s/D = 2.5 x 10^-6/2.5 x 10^-2 = 0.0001 radian.

The resolution of the eye, 0.3 milliradian, is slightly worse than would be expected if the eye were a perfect detector, 0.1 milliradian, where if the black bar fell on one cone, then the white bar on the adjacent cone, and the black bar on the very next cone they eye should be able to resolve the gap between the bars. However, an average person needs a gap that is three times larger than this to resolve the separation of the bars.

Some people however can see at 20/10 so they approach the theoretical limit for human perception.

When the back bars subtend an angle smaller that the resolution of the eye they are seen as an undivided gray square.